Eğer sistemde sürtünme veya benzeri dirençler sebebi ile enerji kaybı ve sönümüne sebep olacak bir etki yok ise titreşim problemi sönümsüz (undamped) olarak adlandırılır. Titreşim problemlerini incelerken sönüm ihmal edilerek çözüm basitleştirilebilir, fakat sönüm etkileri özellikle rezonans durumu için oldukça önemlidir.
Bu makalede sönümsüz tek serbestlik dereceli sistem incelenecek ve örnek çalışma yapılacaktır.
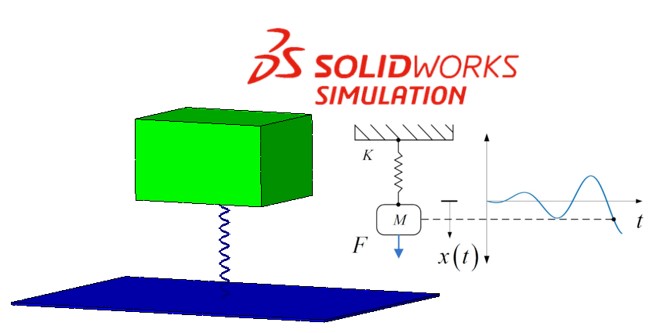
Tek Serbestlik Dereceli Sönümsüz Bir Sistemin Serbest Titreşimleri
Kütle yay sisteminin matematiksel modeli;

Tek serbestlik dereceli sönümsüz bir sistemin hareket denkleminde C=0 ve F(t)=0 kabul edilir. Denklem en son aşağıdaki şeklini alır ;
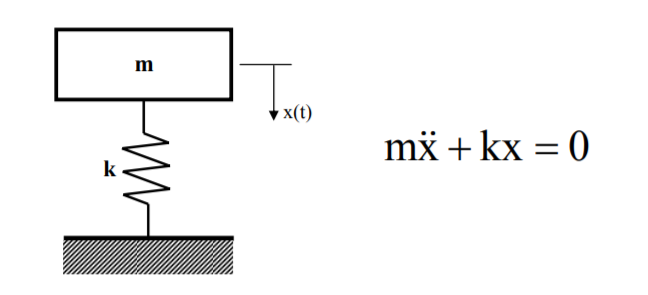
Hareket denkleminin çözümü için x(t) = aest kabulü yapılır ve a ve s sabitleri belirlenir.
Kabul edilen çözüm ve türevleri hareket denkleminde yerine konur;
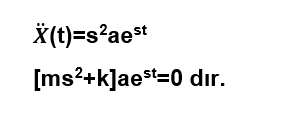
Başlangıçta kabul edilen çözümün geçerli ve işe yarar bir çözüm olabilmesi için aest’nin
sıfırdan farklı olması gereklidir. Bu durumda aest teriminin çarpanı, karakteristik denklem belirtir ve sıfıra eşit olmalıdır ve bu denklemi sıfır yapan s değerleri sistemin özdeğerleri (eigenvalue) olarak adlandırılır ve her iki s değeri de karakteristik denklemi sağlar.
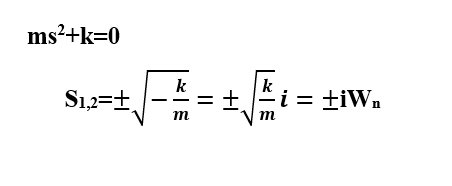
Tek serbestlik dereceli sistemin serbest titreşimlerinin frekansı aşağıdaki gibidir;
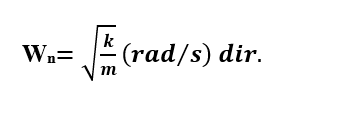 Tek Serbestlik Dereceli Sönümsüz Bir Problemin SOLIDWORKS Simulation ile Doğal Frekansının Hesaplanması
Tek Serbestlik Dereceli Sönümsüz Bir Problemin SOLIDWORKS Simulation ile Doğal Frekansının Hesaplanması
Kütlesi m= 2kg olan ve yay sabiti k=10000N/m olan bir kütle yay sisteminin doğal frekansını teorik formüller aracılığıyla ile hesaplanmasını ve analiz programında nasıl hesaplanacağına dair inceleme gerçekleştirelim.
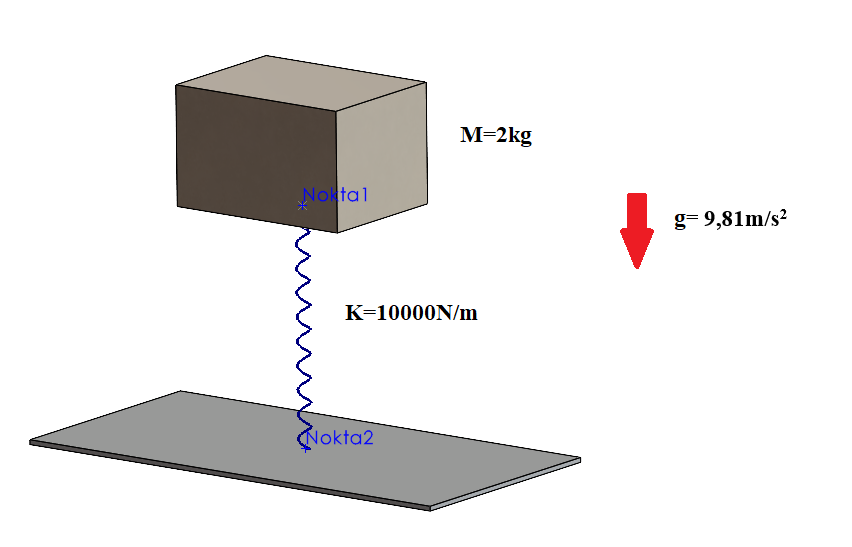
Teorik olarak Doğal Frekansın Hesaplanması
Yukarıda yer alan formülde problemde verilen değerleri kullanarak doğrudan hesaplama yapabiliriz.
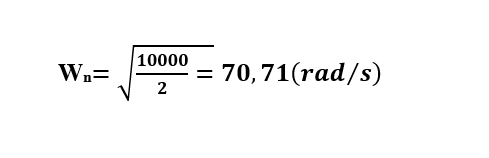
Analiz Programı Aracılığıyla Doğal Frekansın Hesaplanması
Malzeme Bilgisi
Sistemde yer alan parçalar için 1060 Alüminyum Alaşım malzemesi kullanılmıştır. 1060 Alüminyum Alaşım malzemesi mekanik özellikleri aşağıdaki tabloda gösterilmiştir.
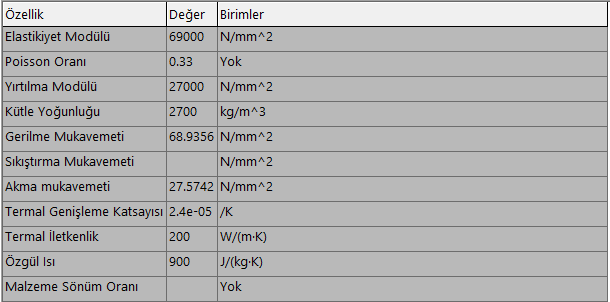
Sınır Koşullar
Program içerisinde yay tanımlaması yapılabilmesi için modelin alt ve üst parçalarında yayın geleceği yerlere nokta ataması yapılmıştır.
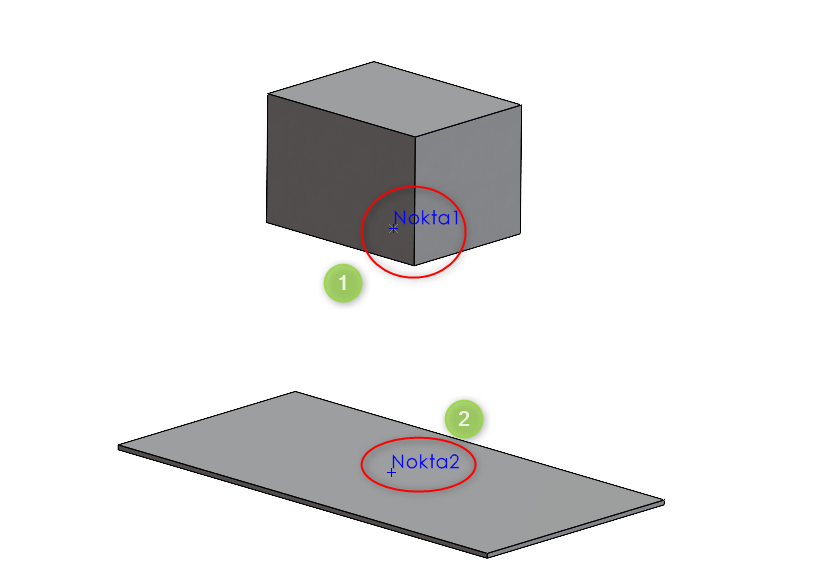
Bağlantı elemanları arasında yer alan yay tanımı seçilerek konumlar arasındaki noktalar seçilmiştir. Problemde verilen yay sabiti değeri burada girilmiştir.
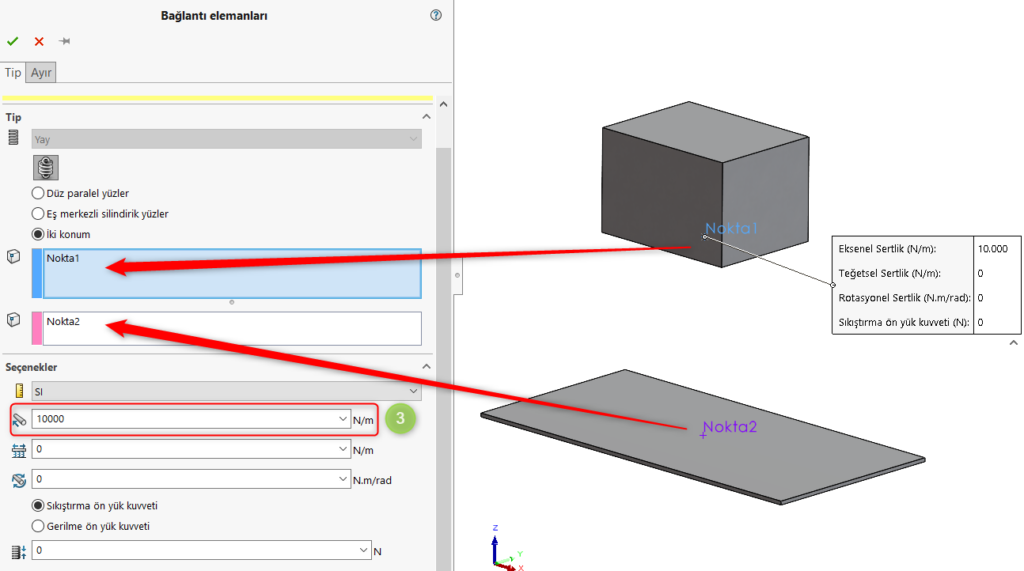
Model alt yüzeyinden sabitleme işlemi yapılmıştır.
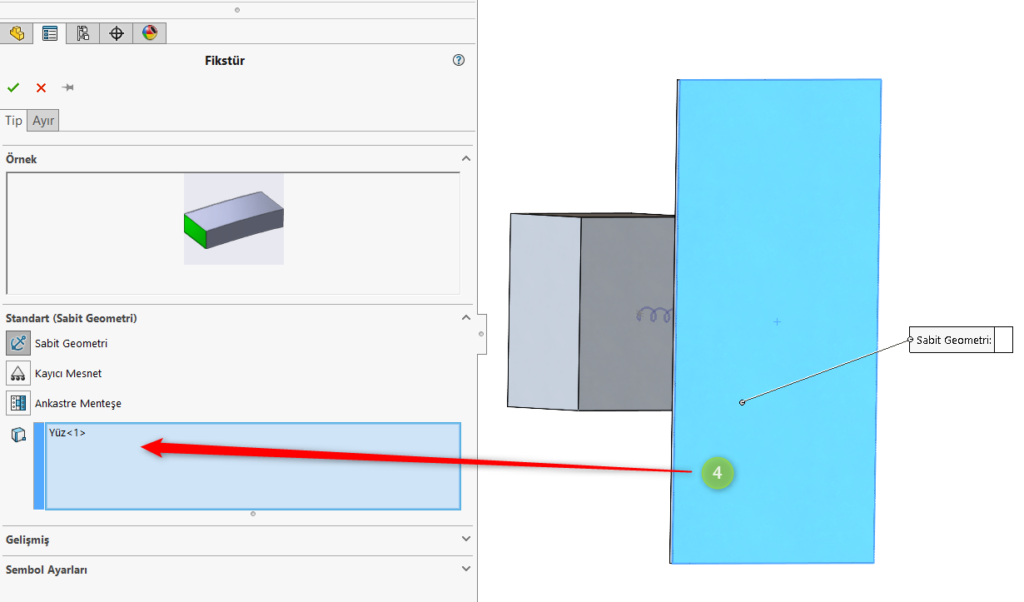
Üst parçanın her yüzeyi seçilerek sadece Z ekseni yönünde hareket edecek şekilde sınırlandırma yapılmıştır.
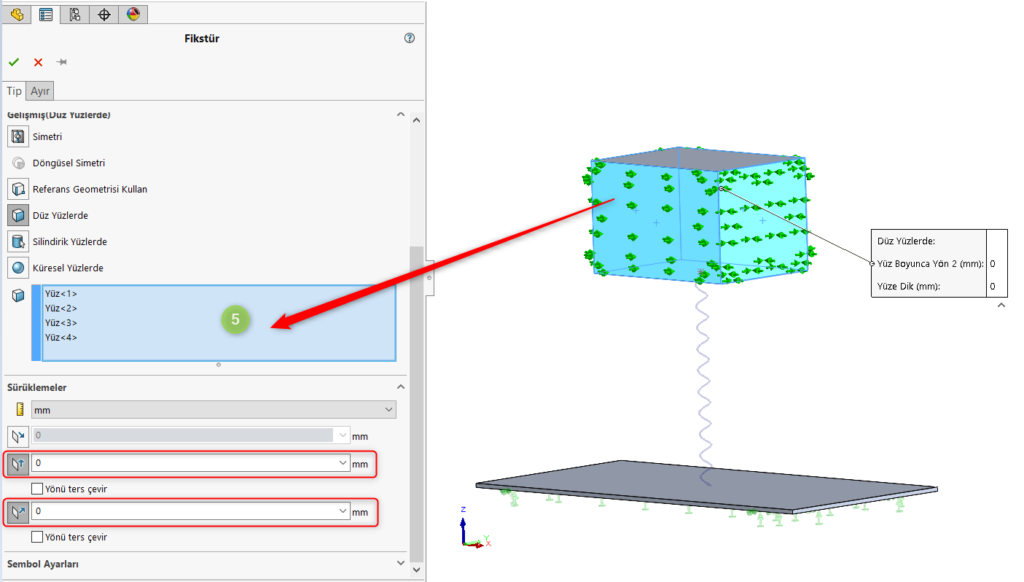
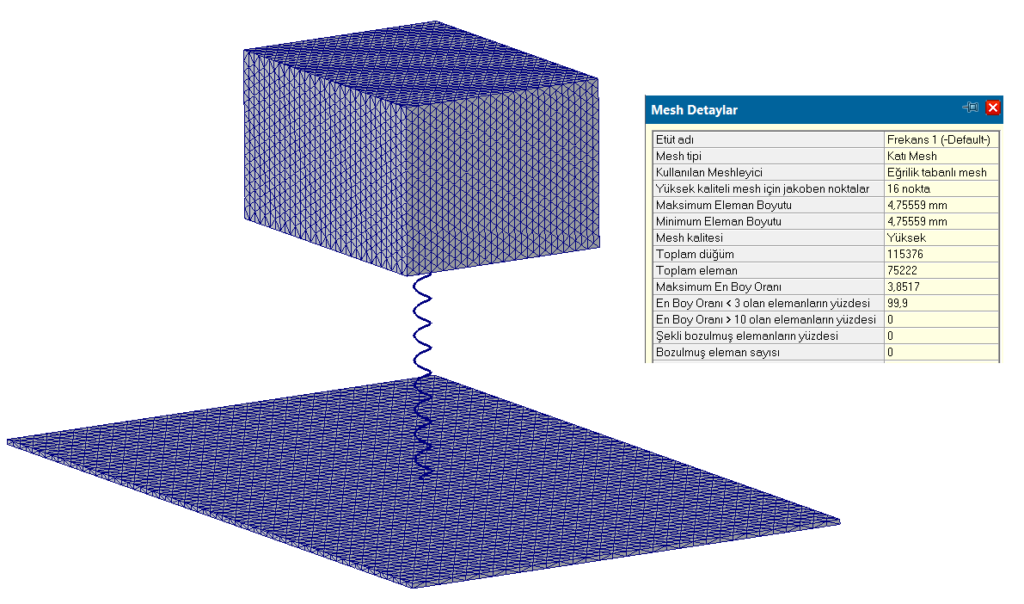
Bu modelde hacim eleman kullanılarak mesh gerçekleştirilmiştir. Yüksek kalite mesh uygulanmıştır. 115376 düğüm(node), 75222 eleman ile mesh atılmıştır. Mesh detayları aşağıdaki görselde gösterilmiştir.
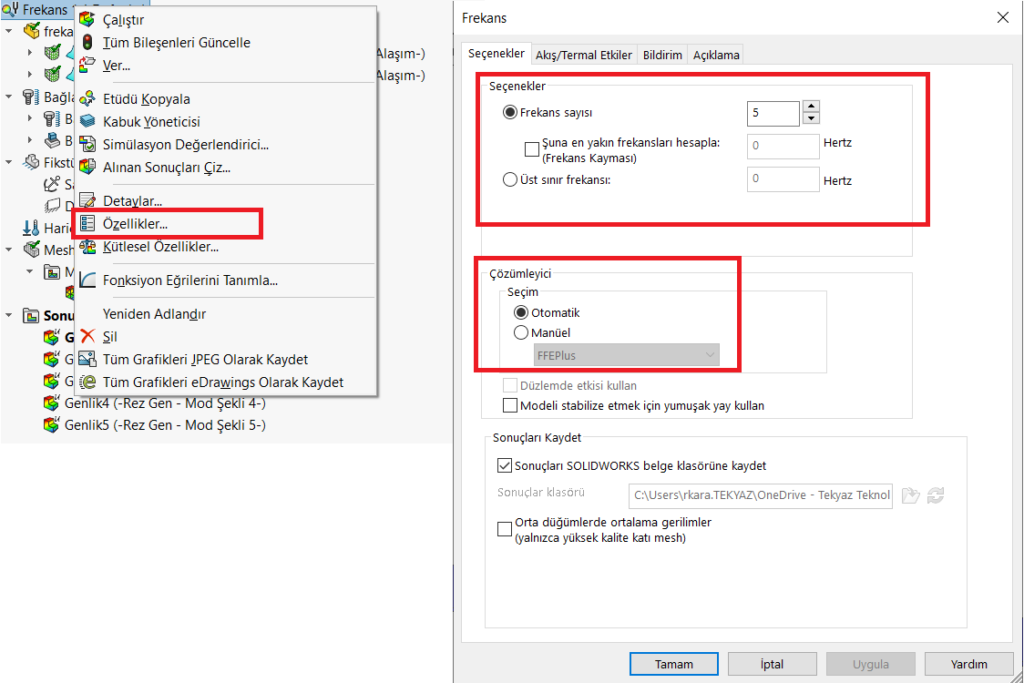
Analiz unsur ağacında analiz başlığına sağ tıklayarak “Özellikler” kısmına girilerek Çözücü tipi ve frekans mod sayısı, üst sınır ve yakın frekans hesaplama seçenekleri düzenlenebilmektedir.
Analiz Sonuçları
Frekans analizi çözüm sonrası frekans değerleri aşağıdaki gibi listelenmiştir. Bu liste Analiz unsur ağacında “Sonuçlar” kısına sağ tıklayıp “Rezonans Frekanslarını Listele” denilerek çıkartılmaktadır.
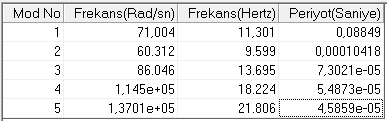
Kütle yay sisteminde ilk doğal frekansı yaklaşık 71,004 Rad/sn çıkmıştır. Rad/sn – Hertz cinsinden dönüşümler aşağıdaki formül aracılığıyla hesaplanmaktadır.
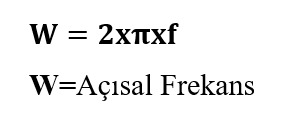
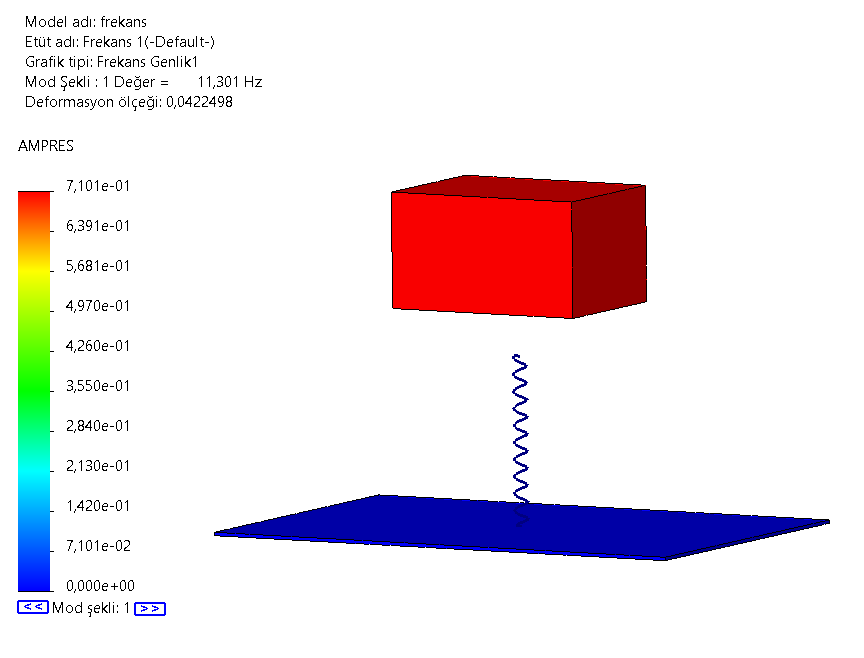
Mod Şekil değişim grafiklerinde, yan kısımda çıkan AMPRES değerleri sayısal olarak incelenmemelidir. Bu değerler model üzerinde oransal olarak bir skala belirlemek adına göz önünde bulundurulmalıdır.
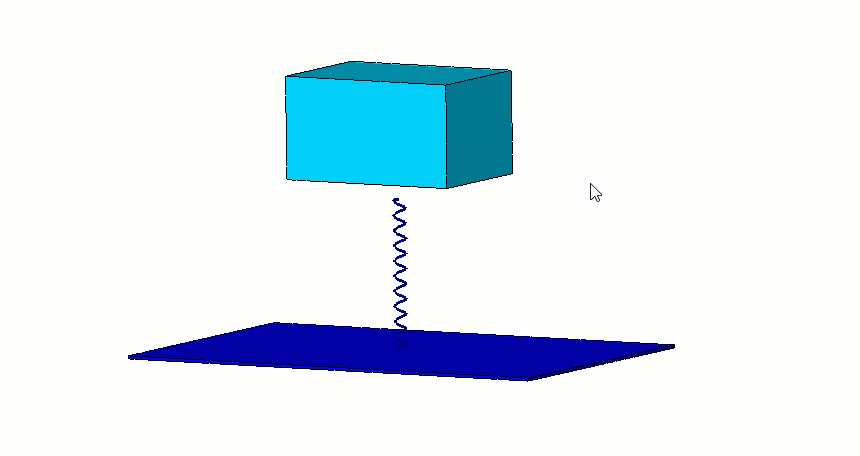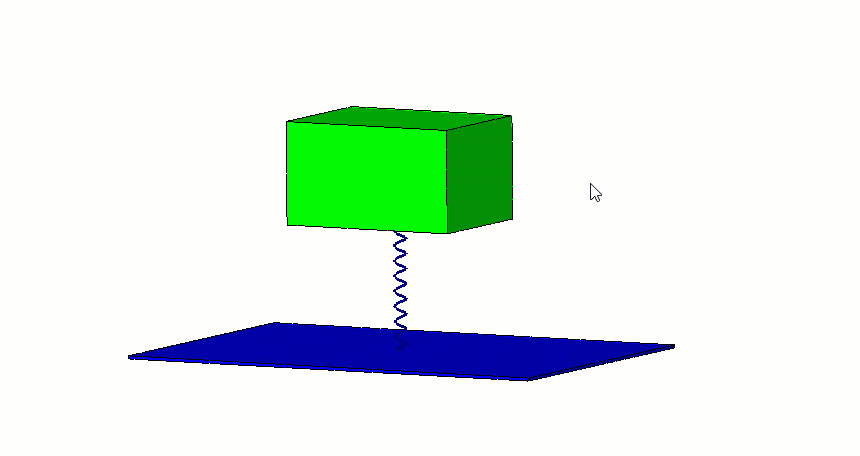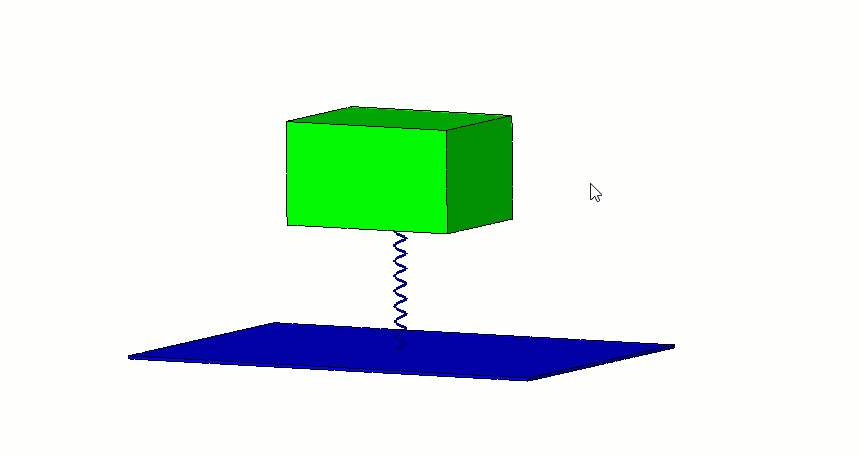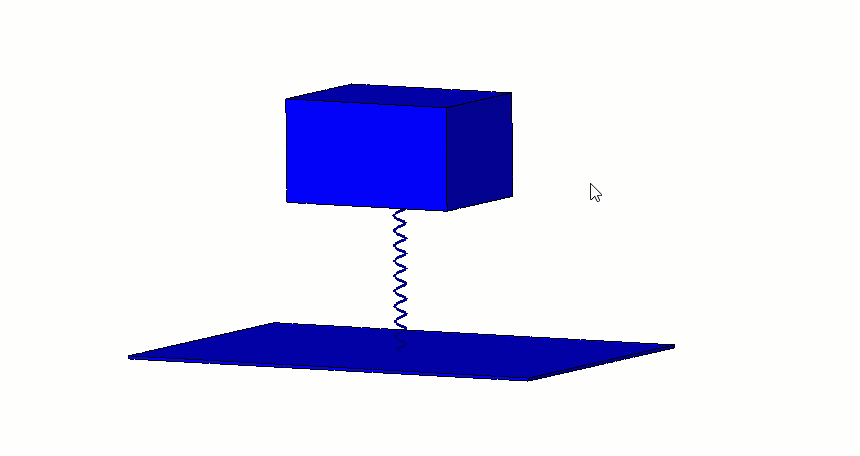
| Teorik Hesaplama | FEA (SOLIDWORKS Simulation) | |
| Doğal Frekans Değeri(Rad/sn) | 70,71 | 71,004 |
Yapılan frekans analizinde teorik sonuçlar ile hesaplanan değer arasındaki fark %1 kadar çıkmıştır. Böylelikle incelenen sistem matematiksel olarak hesaplanmıştır ve analiz işlemleri gerçekleştirilerek doğrulama gerçekleştirilmiştir.
SOLIDWORKS Simulation Professional paket ile frekans analizi gerçekleştirerek modelin titreşim ve deformasyonunu detaylı inceleyebilirsiniz.
KAYNAKLAR:
- ) Theory of Vibrations-W.T.Thomson, Elements of Vibration Analysis-L. Meirovitch, Vibrations of Continuous Systems-S. Rao, Fundamentals of Mechanical Vibrations-S.G. Kelly, Vibration Problems in Engineerin-W.Weaver, S.P. Timoshenko,
D.H. Young, Engineering Vibrations-D.J. Inman, Mühendislik Sistemlerinin Modellenmesi ve Dinamiği-Yücel Ercan