Tasarlanan sistemlerin genel olarak mukavemetine bakılarak güvenli koşul gözlemlenerek yeterlilik koşulu kabul edilmektedir. Ancak ilgili sistemler söz konusu mukavemet koşuluna sürekli olarak maruz kalıyorsa burada ilgili sistemin yorulma, ömür koşulu önem arz etmektedir.
Tekrarlanan yükleme ve boşaltmanın zamanla nesneleri zayıflattığı gözlemlenmiştir. Bu olguya yorulma adı verilir. Her gerilme dalgalanması döngüsü, nesneyi belirli bir ölçüde zayıflatır. Belirli bir döngü sayısı aşıldıktan sonra nesne büyük ölçüde zayıflar ve hasar meydana gelir. Yorulma, metalden üretilenler başta olmak üzere çoğu nesnede meydana gelen hasarın ana sebebidir. Yorulma nedeniyle hasar meydana gelen nesneler arasında dönen parçalar içeren makineler, cıvatalar, uçak kanatları, tüketici ürünleri, sahil platformları, gemiler, otomobil aksları, köprüler, kemikler vb. yer alır.
Doğrusal ve doğrusal olmayan yapısal etütler, yorulma kaynaklı hasarları tahmin etmez. Belirtilen bir kısıtlama ve yük ortamına maruz kalan bir tasarımın vereceği yanıtı hesaplarlar. Analiz varsayımları gözlemleniyorsa ve hesaplanan gerilmeler izin verilen limitler dahilindeyse, yükün kaç kez uygulandığına bakılmaksızın tasarımın bu ortamda güvenli olduğu sonucuna varırlar.
Bir yorulma etüdü tanımlanırken statik, doğrusal olmayan veya doğrusal dinamik etütlerin sonuçları temel alınabilir. Belirli bir konumda yorulma hasarının meydana gelmesi için gereken döngü sayısı, malzemeye ve gerilme dalgalanmalarına bağlıdır. Belirli bir malzemeye yönelik bu bilgiyi, S-N eğrisi adı verilen bir eğri sağlar.
Yorulma mukavemeti, farklı test numunelerine farklı seviyelerde döngüsel gerilmeler uygulanarak ve yorulmaya yol açan döngü sayısı ölçülerek belirlenir. Yorulma veri noktalarının grafiksel temsili, döngüsel gerilme genliği veya alternatif gerilme (S (Stress) – dikey eksen) ile yorulmaya yol açan döngü sayısı (N (Number of cycles) – yatay eksen) karşılaştırılarak gösterilir. Yorulma mukavemeti, belirli bir döngü sayısında yorulma hasarının oluştuğu gerilme olarak tanımlanır. Aşağıda tipik bir S-N eğrisi gösterilmektedir.
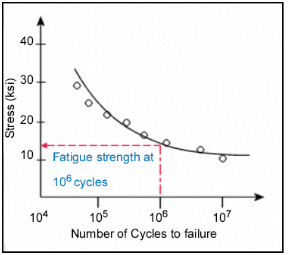
Numuneler, seçilen maksimum döngü sayısında hiçbir hasar oluşmayana kadar bir dizi azaltılan gerilme düzeyinde test edilir. Eğrinin hemen hemen yatay olan bölümü, test malzemesi için yorulmayı veya dayanıklılık limitini tanımlar. Uygulanan gerilme genliği malzemenin dayanıklılık limitinin altındaysa numunenin sonsuz ömre sahip olduğu söylenir. Ancak, alüminyum, magnezyum ve bakır alaşımları gibi birçok demirsiz metal ve alaşımlarda sonlu bir dayanıklılık limiti olmaz ve eğrinin düşük gerilme bölümü yatay bir çizgiyle birleşmez. Bunun yerine bu malzemeler, sürekli olarak azalan bir S-N eğrisi görüntüler.
Bir malzemenin S-N eğrisi, döngüsel gerilme genliklerini (veya alternatif gerilmeyi) belirli bir gerilme oranı R’de hasara yol açmak için gereken döngü sayısıyla karşılaştırarak tanımlar. Gerilme oranı R, minimum döngüsel gerilmenin maksimum döngüsel gerilmeye oranı olarak tanımlanır. Tamamen ters çevrilmiş bir yüklemede, R = -1’dir. Yükleme uygulanıp kaldırıldığında (ters çevrilmediğinde), R=0’dır.
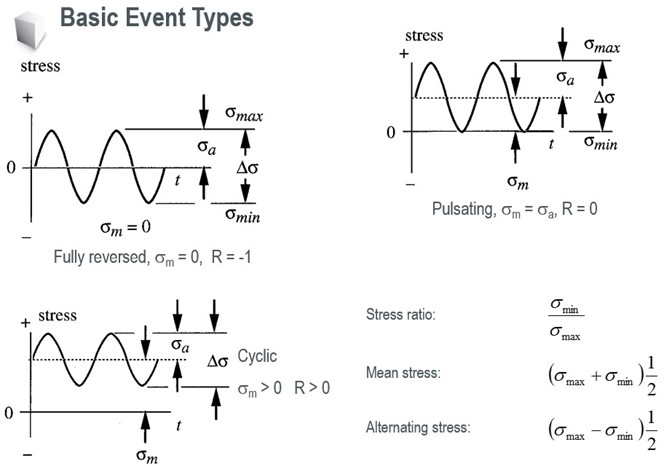
S-N eğrileri, ortalama yorulma ömrüne ya da belirli bir hasar olasılığına dayalıdır. Bir malzeme için S-N eğrisinin oluşturulması, alternatif gerilmeyi ve ortalama gerilmeyi (veya gerilme oranı) istatistiksel olarak değiştirmek ve yorulmaya yol açan döngü sayısını saymak için birçok test yapılmasını gerektirir. S-N eğrilerini oluşturmaya yönelik testler, kontrollü bir yükleme ortamı altında gerçekleştirilir. Çoğu durumda, S-N eğrileri tam ters çevrilmiş gerilme döngüleri üzerinde eksenel olmayan yüklemeyle elde edilir.
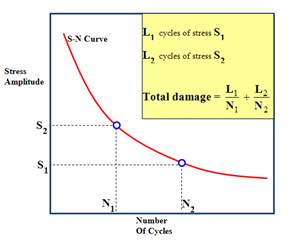
S-N eğrisinin, yorulma hasarının meydana gelmesi için S1 alternatif gerilme değerinde N1 döngü gerekeceğini belirttiğini varsayarsak teori her bir döngünün, yapı ömrünün 1/N1’ini tüketen bir D1 hasar faktörüne neden olduğunu bildirir. Ayrıca, bir yapı S1 alternatif gerilme değerinde n1 döngüye ve S2 alternatif gerilme değerinde n2 döngüye maruz bırakılırsa, toplam hasar faktörü D şu şekilde hesaplanır:
D = (n1/N1 + n2/N2)
Burada N1, S1 koşulu altında hasara neden olmak için gereken döngü sayısıdır ve N2, S2 koşulu altında hasara neden olmak için gereken döngü sayısıdır. Bu kurala Doğrusal Hasar Kuralı veya Miner Kuralı adı verilir. Hasar faktörü (kullanım faktörü de denir), yapının tüketilen ömrünün oranını gösterir. 0,35’lik bir hasar faktörü, yapı ömrünün %35’inin tüketildiği anlamına gelir. Hasar faktörü 1,0’a ulaşınca yorulma kaynaklı hasar meydana gelir.
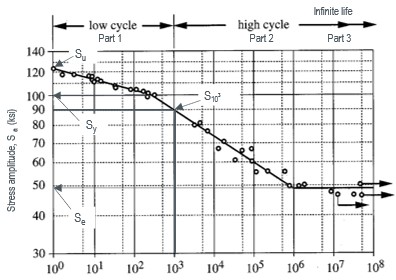
S-N Eğrileri incelendiğinde 1000 döngü ve sonrası yüksek döngüye girerken 1000 döngüden az olan döngüler düşük döngü olarak nitelendirilir. 1,000,000 döngü ve sonrası değerler sonsuz ömre (infinite life) doğru ilerlemekte olup gerilme grafiğinde yüksek değişiklikler gözlemlenmemektedir.
Ortalama Gerilme Düzeltme:
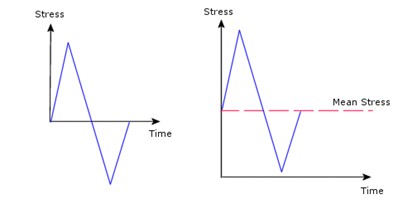
Bir gerilme döngüsünün alternatif gerilme genliği, döngüdeki gerilme aralığının yarısı olarak hesaplanır. Bir gerilme döngüsünün neden olduğu zararın miktarı, alternatif gerilmenin yanı sıra ortalama gerilmeye de bağlıdır. Örneğin, aşağıdaki iki döngü aynı alternatif gerilmeye sahiptir fakat farklı ortalama gerilmelere sahip olmaları nedeniyle farklı miktarlarda zarara neden olurlar.
Ortalama gerilmelerin döngü hatası üzerindeki etkisi, Haigh diyagramı adı verilen aşağıdaki diyagramda gösterilmektedir.
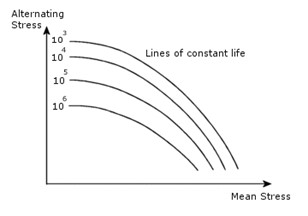
Ortalama gerilme yalnızca yükün tamamen tersine çevrilebilir olduğu durumlarda sıfırdır. Yükle aynı R oranına sahip bir S-N eğrisinin sunulduğu durumlar, bunu en iyi gösteren örneklerdir. Bu örnekte, hiçbir düzeltme gerekmediğinden S-N eğrisi doğrudan kullanılır. Farklı R oranlarına sahip S-N eğrileri tanımlarsanız, yazılım eğriler arasında doğrusal interpolasyon yoluyla ortalama gerilmeyi belirler. Yükün R oranından farklı bir R oranına sahip sadece bir S-N eğrisi sunulursa bir düzeltme gerekir.
SOLIDWORKS Simulation, ortalama gerilmeyi hesaplamak için her zaman Von-Mises gerilmesini kullanır. Von-Mises pozitif bir miktar olduğu için program, ilişkili ortalama gerilmenin hesaplanması amacıyla birincil gerilmenin işaretini en büyük cebirsel büyüklüğe atar.
Bu sebeple farklı stres değerleri olarak stres yoğunluğu P1-P3 ve maksimum asal stres P1 seçenekleri modelde çıkan yüksek gerilme değerlerine göre tercih edilebilir.
Düzeltme yöntemlerini açıklamadan önce bir gerilme döngüsüne yönelik aşağıdaki değişkenler tanımlanırsa:
Smaks = maksimum gerilme
Smin = minimum gerilme
ΔS = gerilme aralığı = Smaks – Smin
Sa = alternatif gerilme = (Smaks – Smin)/2
Sortalama = ortalama gerilme = (Smaks + Smin)/2
R = gerilme oranı = Smin/Smaks
A = genlik oranı = Sa/Sortalama
Bazı genel yükler için gerilme ve genlik oranları listelenmiştir:
Tamamen ters çevrilmiş R = -1, A = sonsuz
Sıfırdan maksimuma R = 0, A = 1
Sıfırdan Minimuma R = sonsuz, A = -1
Düzeltme Yöntemleri:
Sca = düzeltilen alternatif gerilme (sıfır ortalamaya dayalı.),
Sy = akma gerilmei ve
Su = nihai mukavemet

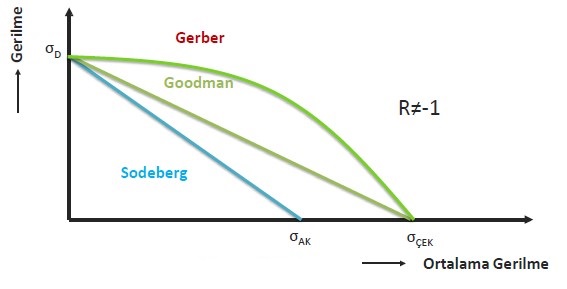
Ortalama gerilme düzeltme yöntemleri Goodman, Gerber ve Soderberg şeklindedir. Gevrek malzemeler için Goodman, sünek malzemeler için Gerber metodu tercih edilmektedir. Soderberg yöntemi en muhafazakar yöntemdir. Sünek malzemeler için yine Soderberg yöntemi de tercih edilmektedir.
Tasarlamış olduğunuz ürün ve modellerinizin Yorulma-Ömür tayinini analiz çözümlerimizle gerçekleştirebilirsiniz. SOLIDWORKS Simulation paketlerinin tümünde Yorulma-Ömür analizi yapabilirsiniz.
Yorulma-Ömür ile ilgili diğer içeriklerimize aşağıdaki linklerden erişebilirsiniz.
Neden Yorulma Analizi Yapmalıyız ?
Yorulma Ömrünü Etkileyen Çevresel ve Geometrik Faktörler
Yüksek Çevrimli Ve Düşük Çevrimli Yorulma Analizi